 |
|
You are not logged in! F.A.Q Log in Register |
 |

|
 |
recycle ...and 251 guests Last 5 registered Oplandisks nothingstar N_loop yipe foxtrotromeo Browse members... |
 |
Messages 2619639 Today 0 Topics 127928 |
|
|||||||||
| |||||||||
|
General number field sieve From Wikipedia, the free encyclopedia. In mathematics, the general number field sieve is the most efficient algorithm known for factoring integers. It uses steps to factor integer n (see Big O notation). It is derived from the special number field sieve. When the term number field sieve is used without qualification, it refers to the general number field sieve. [edit] Method We choose two irreducible polynomials f(x) and g(x) with common root m mod n; they will be of order of m, while having small degrees d and e of our polynomials. It is not known what is the best way to choose the polynomials, but usually it is done by picking a degree d for a polynomial and considering expansion of n in basis m where m is of order n1/d. The point is to get coefficients of f and g as small as possible. Now, we consider number field rings Z[r1] and Z[r2] where r1 and r2 are roots of polynomials f and g, and look for values a and b such that r = bd·f(a/b) and s = be·g(a/b) are smooth relative to the chosen basis of primes. If a and b are small, r and s will be too (but at least of order of m), and we have a better chance for them to be smooth at the same time. Having enough such pairs, using Gaussian elimination, we can get products of certain r and of corresponding s to be squares at the same time. We need a slightly stronger condition — that they are norms of squares in our number fields, but we can get that condition by this method too. Each r is a norm of a- r1*b and hence we get that product of corresponding factors a- r1*b is a square in Z[r1], with a "square root" which can be determined (as a product of known factors in Z[r1]) — it will typically be represented as a nonrational algebraic number. Similarly, we get that product of factors a- r2*b is a square in Z[r2], with a "square root" which we can also compute. Since m is root of both f and g mod n, there are homomorphisms from the rings Z[r1] and Z[r2] |
|||||||||
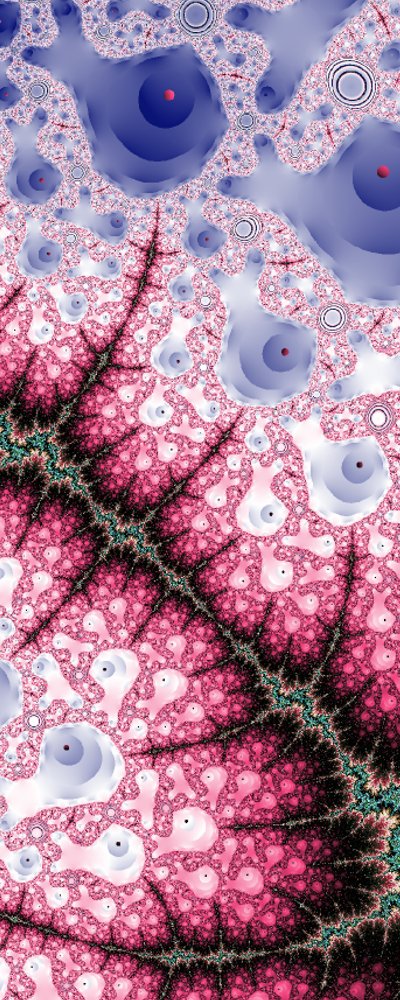
| Attached picture | |||||||||
|
|||||||||
|
|
|||||||||
| |||||||||
|
don`t understand a thing, but it looks greeeeeat. |
|||||||||
|
|
|||||||||
| |||||||||
|
Well, DUUH! |
|||||||||
|
|
|||||||||
| |||||||||
|
erm, what on earth?! perhaps that sort of thing should be best left in the laboratory with the lab rats...I mean weasel |
|||||||||
|
|
|||||||||
| |||||||||
|
i hate math |
|||||||||
|
|
|||||||||
| |||||||||
|
I love math, but I'm no longer very strong at it.. |
|||||||||
|
|
|||||||||
| |||||||||
|
if you love math i really admire you, but this shit gave me a lot of head-fuck back in the school days. |
|||||||||
|
|
|||||||||
| |||||||||
|
at least in the united states, high school (and prior) math education is a wreck. It is just a mess of basic computation tools for engineering tasks. Real mathematics is all about structure, and structure is all about exactness and correlation. If these concepts sound beautiful to you, I suggest finding an 'advanced' math book, and digging in, however long (or short!!) it takes. For instance some basics of 'contemporary abstract algebra' (group theory). |
|||||||||
|
|
|||||||||
| |||||||||
|
a mathematician told me once that "high" math is more like philosophy, very abstract and complex. i`m into abstract and complex, but in the humanities. so, no "digging into" a math book, unless wit a gun pointed at my head. :-)) |
|||||||||
|
|
|||||||||
| |||||||||
|
People should approach math from a humanist point of view, and the humanities with the rigour of algebraic structures. |
|||||||||
|
|
|||||||||
| |||||||||
|
*backs away* okay you've lost me now... -_- |
|||||||||
|
|
|||||||||
| |||||||||
|
I read a book once, probably with chaos in the title, but it was about math in a nonmathematical way; no equations etc. Just weird things like flower petals being in fibonaci numbers or watching a brick suddenly falling from a building and concluding that events in time generally happen in leaps rather than gradually (same in evolution). |
|||||||||
|
|
|||||||||
| |||||||||
|
actual some math (for example category theory... logical realms) gets classified as philosophy. I highly recommend looking into formal logic some time, it's god damned sweet may I also interest you in a set of flowers, or an encyclopedia? I also know some beautiful women.. |
|||||||||
|
|
|||||||||
| |||||||||
|
Actually I should look into "proofs" like in geometry. I remember liking those and I bet there are some really insane ones that could inspire me to get more into math. |
|||||||||
|
|
|||||||||
| |||||||||
|
oh shit, now you've done it. I took my first course in algebra last semester and loved it. We didn't cover much ring or field theory, so I'll be digging into that this summer. The stuff just makes my brain feel good.. I love how many different clever and at least eventually intuitive ways there are to prove most things. |
|||||||||
|
|
|||||||||
| |||||||||
|
Like I said, what most people think of as math is just engineering crap. I'm not saying I don't enjoy computation, but I have a new found love for it with a better understanding with what goes underneath. But yeah 'real' math rules. Even the simplest things. For instance consider the set of all positive integers. I can define/construct this set using two simple rules: 1) the set contains the number 1 2) the set contains the successive integer to every integer in the set. This is also called the set of natural numbers or the inductive set, and leads to the very fundamental proof concept 'induction'. |
|||||||||
|
|
|||||||||
|
Messageboard index
|
|||||||||




